ЕКІ ЕСЕ ДЕРЛІК ДӨҢЕС ФУНКЦИЯЛАРДЫҢ КЕЙБІР КЛАСТАРЫ ТУРАЛЫ

Мақалада авторлардың алдыңғы зерттеу жұмыстарының бірінде алынған нәтижелер негізінде (Қазақстан-Британ техникалық университетінің хабаршысы, 2024, 21(2), б. 127-138), f(z) функцияларының бірлік шеңберіндегі екі есе дерлік дөңес класы енгізіліп, төмендегі шарттардың көмегімен зерттеу жұмысы жүргізілді:

мұндағы f(z), g(z) және h(z) функцияларында 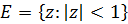, және h(z) функциясы дөңес. Бұл сыныпта бұрмалау, айналу және дөңес радиус теоремалары орнатылған. Ерекше жағдайларда екі есе дерлік дөңес және дөңес функциялар үшін бұрын белгілі және бірқатар жаңа түпнұсқа нәтижелер алынды. Осы сыныпқа сүйене отырып, өсу теоремасы мен жұлдыз тәрізді радиусы табылған жұлдыз тәрізді функциялардың екі еселенген класы енгізілді. Параметрлердің нақты мәндерінде жұлдыз тәрізді функциялар үшін бұрын белгілі нәтижелер бар.

1. Майер Ф.Ф., Тастанов М.Г., Утемисова А.А., Ысмағұл Р.С. Точные оценки регулярных функций и радиусы выпуклости и звездообразности некоторых классов звездообразных и почти звездообразных функций // Вестник Казахстанско-Британского технического университета. – 2024. – Vol. 21. – No. 2. – С. 127–138. https://doi.org/10.55452/1998-6688-2024-21-2-127-138.

2. Suffridge T.J. Some remarks on convex maps of the unit disk // Duke Math. J. – 1970. – No. 37. – P. 755–777. https://doi.org/10.1215/S0012-7094-70-03792-0.

3. Kaplan W. Close-to-convex schlicht functions // Michigan Math. J. – 1952. – Vol.1. – No. 2. – P. 169–185. https://doi.org/10.1307/mmj/1028988895.

4. Reade M.O. The coefficients of close-to-convex functions // Duke Math. J. – 1956. – Vol. 23. – No. 3. – P. 459–462. https://doi.org/10.1215/S0012-7094-56-02342-0.

5. Renyi A. Some remarks on univalent functions // An. Univ. Maria Curie-Sklodowska, Sec. – 1959. – A.3. – P. 111–121. http://sci-gems.math.bas.bg:8080/jspui/bitstream/10525/2878/1/1959-111-121.pdf.

6. Hengartner W., Schober G. Analytic functions close to mappings convex in one direction. // Proc. Amer. Math. Soc. – 1971. – Vol. 28. – No. 2. – P. 519–524. https://www.ams.org/journals/proc/1971-028-02/S0002-9939-1971-0277704-9/S0002-9939-1971-0277704-9.pdf

7. Dorff M., Naraniecka I., Szynal J. Doubly close-to-convex functions // J. Math. Anal. Appl. – 2004. – No. 290. – P. 55–62. https://doi.org/10.1016/j.jmaa.2003.08.050.

8. Raducanu D. Bounded doubly close-to-convex functions. – Hindawi Publishing Corporation, Abstract and Applied Analysis. – 2014. – Article ID 804095. – P. 7. http://dx.doi.org/10.1155/2014/804095.

9. Krzyz J. On the derivative of close-to-convex functions // Colloq. Math. – 1963. – No. 10. – P. 143–146.

10. Hayman W.K. Multivalent functions // Cambridge Tracts in Mathematics. – 1994. – No. 110. – 276 p.

11. Vasudevarao A., Sokół J., Thomas D.K. On a close-to-convex analogue of certain starlike functions // Bull. Aust. Math. Soc. – 2020. – Vol. 102. – No. 2. – P. 268–281. https://doi.org/10.1017/S0004972719001606.

12. Ratti J.S. The radius of convexity of certain analytic functions II // Intern. J. of Math. and Math. Scie. – 1980. – Vol. 3. – No. 3. – P. 483–489. https://doi.org/10.1155/s0161171280000361.

13. Reade M.O. On close-to-close univalent functions // Michigan Math. J. – 1955. – No. 3. – P. 59–62.

14. El-Faqeer A.S.A., Mohd M.H., Ravichandran V., Supramaniam S. Starlikeness of certain analytic functions // arXiv preprint arXiv:2006.11734. – 2020. https://doi.org/10.48550/arXiv.2006.11734.

15. Sebastianc A., Ravichandran V. Radius of starlikeness of certain analytic functions // Math. Slovaca. – 2021. – Vol. 71. – No. 1. – P. 83–104. https://doi.org/10.1515/ms-2017-0454.

16. Khatter K., Lee S.K., Ravichandran V. Radius of starlikeness for classes of analytic functions // arXiv preprint arXiv:2006.11744. – 2020. https://doi.org/10.48550/arXiv.2006.11744.