ON SOME CLASSES OF DOUBLY NEARLY CONVEX FUNCTIONS

 Based on the results obtained by the authors in one of the previous articles (Bulletin of the Kazakh-British Technical University, 2024, 21(2), pp.127-138), the class of doubly close-to-convex in the unit disk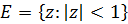
of the functions f(z), set using the conditions 

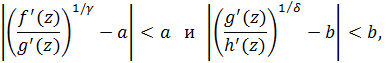
 where the functions f(z), g(z) and h(z) have expansions of the form 

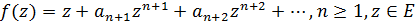
, and the function h(z) is convex. In this class, the theorems of distortion, rotation and radius of convexity are established. In particular cases, we obtain both a number of previously known and a number of new original results for doubly close-to-convex and close-to-convex functions. Based on this class, a class of doubly close-to-starlike functions is introduced, for which the growth theorem and the star radius are found. For specific values of the parameters previously known results for close-to-starlike functions are obtained.

1. Maiyer F.F., Tastanov M.G., Utemissova A.A. and Ysmagul R.S. Exact estimates of regular functions and radii of convexity and starlikeness of some classes of starlike and close-to-starlike functions. Herald of the Kazakh-British technical university, 21(2), 127–138 (2024). [In Russian]. https://doi.org/10.55452/1998-6688-2024-21-2-127-138.

2. Suffridge T.J. Some remarks on convex maps of the unit disk. Duke Math. J., 37, 755–777 (1970). https://doi.org/10.1215/S0012-7094-70-03792-0.

3. Kaplan W. Close-to-convex schlicht functions. Michigan Math. J., 1(2), 169–185 (1952). https://doi.org/10.1307/mmj/1028988895.

4. Reade M.O. The coefficients of close-to-convex functions. Duke Math. J., 23(3), 459–462 (1956). https://doi.org/10.1215/S0012-7094-56-02342-0.

5. Renyi A. Some remarks on univalent functions. An. Univ. Maria Curie-Sklodowska, Sec., A.3, 111–121 (1959). http://sci-gems.math.bas.bg:8080/jspui/bitstream/10525/2878/1/1959-111-121.pdf

6. Hengartner W. and Schober G. Analytic functions close to mappings convex in one direction. Proc. Amer. Math. Soc., 28(2), 519–524 (1971). https://www.ams.org/journals/proc/1971-028-02/S0002-9939-1971-0277704-9/S0002-9939-1971-0277704-9.pdf

7. Dorff M., Naraniecka I. and Szynal J. Doubly close-to-convex functions. J. Math. Anal. Appl., 290, 55–62 (2004). https://doi.org/10.1016/j.jmaa.2003.08.050

8. Raducanu D. Bounded doubly close-to-convex functions. Hindawi Publishing Corporation, Abstract and Applied Analysis, Article ID 804095, 7 p. (2014). http://dx.doi.org/10.1155/2014/804095.

9. Krzyz J. On the derivative of close-to-convex functions. Colloq. Math., 10, 143–146 (1963).

10. Hayman W.K. Multivalent functions. Cambridge Tracts in Mathematics, 110, 276 p. (1994)

11. Vasudevarao A., Sokół J. and Thomas D.K. On a close-to-convex analogue of certain starlike functions. Bull. Aust. Math. Soc., 102, Is. 2, 268-281 (2020). https://doi.org/10.1017/S0004972719001606

12. Ratti J.S. The radius of convexity of certain analytic functions II. Intern. J. of Math. and Math. Scie., 3(3), 483–489 (1980). https://doi.org/10.1155/s0161171280000361

13. Reade M.O. On close-to-close univalent functions. Michigan Math. J., 3, 59-62 (1955).

14. El-Faqeer A.S.A., Mohd M.H., Ravichandran V. and Supramaniam S. Starlikeness of certain analytic functions. arXiv preprint arXiv:2006.11734 (2020). https://doi.org/10.48550/arXiv.2006.11734.

15. Sebastianc A. and Ravichandran V. Radius of starlikeness of certain analytic functions. Math. Slovaca, 71(1), 83-104 (2021). https://doi.org/10.1515/ms-2017-0454.

16. Khatter K., Lee S. K. and Ravichandran V. Radius of starlikeness for classes of analytic functions. arXiv preprint arXiv:2006.11744 (2020). https://doi.org/10.48550/arXiv.2006.11744