О НЕКОТОРЫХ КЛАССАХ ДВАЖДЫ ПОЧТИ ВЫПУКЛЫХ ФУНКЦИЙ

На основе результатов, полученных авторами в одной из предыдущих статей (Вестник Казахстанско-Британского технического университета, 2024, 21(2), С.127–138), вводится и исследуется класс дважды почти выпуклых в единичном круге функций , заданный с помощью условий

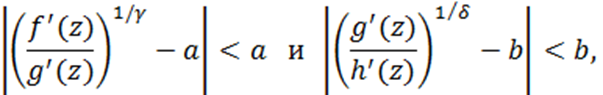
где функции , и имеют разложения вида 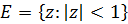, и функция является выпуклой. В данном классе установлены теоремы искажения, вращения и радиус выпуклости. В частных случаях получается как ряд ранее известных, так и ряд новых оригинальных результатов для дважды почти выпуклых и почти выпуклых функций. На основе данного класса вводится класс дважды почти звездообразных функций, для которого найдены теорема роста и радиус звездообразности. При конкретных значениях параметров получаются ранее известные результаты для почти звездообразных функций.

1. Майер Ф.Ф., Тастанов М.Г., Утемисова А.А., Ысмағұл Р.С. Точные оценки регулярных функций и радиусы выпуклости и звездообразности некоторых классов звездообразных и почти звездообразных функций // Вестник Казахстанско-Британского технического университета. – 2024. – Vol. 21. – No. 2. – С. 127–138. https://doi.org/10.55452/1998-6688-2024-21-2-127-138.

2. Suffridge T.J. Some remarks on convex maps of the unit disk // Duke Math. J. – 1970. – No. 37. – P. 755–777. https://doi.org/10.1215/S0012-7094-70-03792-0.

3. Kaplan W. Close-to-convex schlicht functions // Michigan Math. J. – 1952. – Vol.1. – No. 2. – P. 169–185. https://doi.org/10.1307/mmj/1028988895.

4. Reade M.O. The coefficients of close-to-convex functions // Duke Math. J. – 1956. – Vol. 23. – No. 3. – P. 459–462. https://doi.org/10.1215/S0012-7094-56-02342-0.

5. Renyi A. Some remarks on univalent functions // An. Univ. Maria Curie-Sklodowska, Sec. – 1959. – A.3. – P. 111–121. http://sci-gems.math.bas.bg:8080/jspui/bitstream/10525/2878/1/1959-111-121.pdf.

6. Hengartner W., Schober G. Analytic functions close to mappings convex in one direction. // Proc. Amer. Math. Soc. – 1971. – Vol. 28. – No. 2. – P. 519–524. https://www.ams.org/journals/proc/1971-028-02/S0002-9939-1971-0277704-9/S0002-9939-1971-0277704-9.pdf

7. Dorff M., Naraniecka I., Szynal J. Doubly close-to-convex functions // J. Math. Anal. Appl. – 2004. – No. 290. – P. 55–62. https://doi.org/10.1016/j.jmaa.2003.08.050.

8. Raducanu D. Bounded doubly close-to-convex functions. – Hindawi Publishing Corporation, Abstract and Applied Analysis. – 2014. – Article ID 804095. – P. 7. http://dx.doi.org/10.1155/2014/804095.

9. Krzyz J. On the derivative of close-to-convex functions // Colloq. Math. – 1963. – No. 10. – P. 143–146.

10. Hayman W.K. Multivalent functions // Cambridge Tracts in Mathematics. – 1994. – No. 110. – 276 p.

11. Vasudevarao A., Sokół J., Thomas D.K. On a close-to-convex analogue of certain starlike functions // Bull. Aust. Math. Soc. – 2020. – Vol. 102. – No. 2. – P. 268–281. https://doi.org/10.1017/S0004972719001606.

12. Ratti J.S. The radius of convexity of certain analytic functions II // Intern. J. of Math. and Math. Scie. – 1980. – Vol. 3. – No. 3. – P. 483–489. https://doi.org/10.1155/s0161171280000361.

13. Reade M.O. On close-to-close univalent functions // Michigan Math. J. – 1955. – No. 3. – P. 59–62.

14. El-Faqeer A.S.A., Mohd M.H., Ravichandran V., Supramaniam S. Starlikeness of certain analytic functions // arXiv preprint arXiv:2006.11734. – 2020. https://doi.org/10.48550/arXiv.2006.11734.

15. Sebastianc A., Ravichandran V. Radius of starlikeness of certain analytic functions // Math. Slovaca. – 2021. – Vol. 71. – No. 1. – P. 83–104. https://doi.org/10.1515/ms-2017-0454.

16. Khatter K., Lee S.K., Ravichandran V. Radius of starlikeness for classes of analytic functions // arXiv preprint arXiv:2006.11744. – 2020. https://doi.org/10.48550/arXiv.2006.11744.