ОКРЕСТНОСТИ В СЛАБО УПОРОДЯЧЕННО МИНИМАЛЬНЫХ ТЕОРИЯХ

В данной работе исследуются окрестности, слабая ортогональность и почти ортогональность полных неалгебраических 1-типов в слабо упорядоченных минимальных (слабо о-минимальных) теориях. Окрестности вводятся как инструмент для описания локального поведения реализаций типов и обобщения понятия алгебраического замыкания внутри типа. Их использование позволяет выявить различия между типами и уточнить структуру их взаимодействия. Мы формулируем и доказываем основные свойства окрестностей. В частности, установлено, что 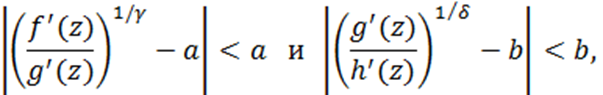 . На основе этих результатов изучаются соотношения между слабой ортогональностью и почти ортогональностью типов. В частности, получены критерии, описывающие их эквивалентность, симметричность и поведение для различных классов типов (иррациональных, квазисолитарных и квазирациональных). Таким образом, работа вносит вклад в уточнение и развитие понятий ортогональности для слабо о-минимальных теорий. Также показано, что для некоторых классов слабо о-минимальных теорий слабая и почти ортогональность совпадают. Полученные результаты предоставляют новые инструменты для анализа геометрии типов в слабо o-минимальных теориях и открывают перспективы применения в дальнейшем исследовании структур слабо о-минимального типа. Кроме того, предложенные подходы могут быть использованы для сопоставления с более общими классами теорий.

1. Baizhanov, B.S., and Verbovskii, V.V. O-stable theories. Algebra and Logic, 50 (3), 211–225 (2011).

2. Baizhanov, B.S. Types in weakly o-minimal theories. 1st Congress of Kazakhstan Mathematicians (11–14 September 1996), Shymkent, p. 177 (1996).

3. Baizhanov, B.S. One-types in weakly o-minimal theories. Proceedings of Informatics and Control Problems Institute, Almaty, pp. 77–90 (1996).

4. Marker, D. Omitting types in o-minimal theories. Journal of Symbolic Logic, 51 (1), 63–74 (1986). https://doi.org/10.2307/2273943

5. Baizhanov, B.S. Orthogonality of one-types in weakly o-minimal theories. In: Pinus, A.C., and Ponomaryov, K.N. (eds.) Algebra and Model Theory. Novosibirsk State Technical University, pp. 5–28 (1999).

6. Baizhanov, B.S., and Tazabekova, N.S. Essential kinds of 1-types over sets of models of weakly o-minimal theories. Kazakh Mathematical Journal, 23 (4), (2023). https://doi.org/10.70474/ckvn1r44

7. Henkin, L. The completeness of the first-order functional calculus. Journal of Symbolic Logic, 14 (3), 159–166 (1949).

8. Shelah, S. Classification theory and the number of non-isomorphic models. North Holland (1978).

9. Baldwin, J. Fundamentals of stability theory. Springer-Verlag (1988).

10. Baizhanov, B.S. Expansion of a model of a weakly o-minimal theory by a family of unary predicates. Journal of Symbolic Logic, 66, 1382–1414 (2001). https://doi.org/10.2307/2695114

11. Baizhanov, B., Umbetbayev, O., and Zambarnaya, T. Non-orthogonality of 1-types in theories with a linear order. Bulletin of Irkutsk State University. Series “Mathematics” (accepted for publication).

12. Baizhanov, B.S. Classification of one-types in weakly o-minimal theories and its corollaries. Preprint (1996).

13. Baizhanov, B.S. Expansion of an o-minimal model by unary convex predicates. Researches in theory of algebraic systems, Karaganda (1995).

14. Kulpehsov, B.Sh. Weak o-minimality of a linearly ordered structure. Researches in theory of algebraic systems, Karaganda, 61–67 (1995).

15. Baizhanov, B.S., Sudoplatov, S.V., and Verbovskiy, V.V. Conditions for non-symmetric relations of semi-isolation. Siberian Electronic Mathematical Reports, 9, 161–184 (2012).

16. Dickmann, M.A. Elimination of quantifiers for ordered valuation rings. Proceedings of the 3rd Easter Model Theory Conference, Gross Koris, Berlin (1985).

17. van den Dries, L. Remarks on Tarski’s problem concerning (R, +, ·, exp). Studies in Logic and the Foundations of Mathematics, 112, 97–121 (1984). https://doi.org/10.1016/S0049-237X(08)71811-1

18. Laskowski, M., and Steinhorn, Ch. On o-minimal expansions of Archimedean ordered groups. Journal of Symbolic Logic, 60, 817–878 (1995). https://doi.org/10.2307/2275758

19. Lascar, D., and Poizat, B. An introduction to forking. Journal of Symbolic Logic, 44, 330–350 (1979).

20. Mayer, L. Vaught’s conjecture for o-minimal theories. Journal of Symbolic Logic, 53, 146–159 (1988). https://doi.org/10.2307/2274434

21. Marker, D., and Steinhorn, Ch. Definable types in o-minimal theories. Journal of Symbolic Logic, 59, 185–198 (1994). https://doi.org/10.2307/2275260

22. Macpherson, D., Marker, D., and Steinhorn, Ch. Weakly o-minimal structures and real closed fields. Transactions of the American Mathematical Society, 352 (12), 5435–5483 (2000). https://doi.org/10.2307/2275260