О РАЗРЕШИМОСТИ НЕЛОКАЛЬНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ИНВОЛЮЦИЕЙ

В данной научной работе рассматривается нелокальная краевая задача для одного класса интегро-дифференциальных уравнений, в структуре которых присутствует инволютивное преобразование. Основное внимание сосредоточено на применении метода параметризации, разработанного и предложенного профессором Д. Джумабаевым, целью которого является исследование условий существования и единственности решения для подобного рода задач, а также определение спектра собственных значений соответствующей краевой задачи. Как известно из теории, задача Коши для уравнений, содержащих инволюции, не всегда имеет единственное решение. Для преодоления данной трудности вводятся параметры 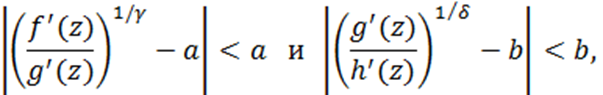 в середине рассматриваемого отрезка и осуществляется преобразование 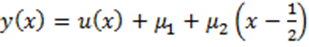, которое обеспечивает существование единственного решения задачи Коши. Это преобразование позволяет разделить исходную нелокальную краевую задачу на две части: во-первых, на специальную задачу Коши и, во-вторых, на систему линейных алгебраических уравнений относительно введенных параметров. После подстановки решения в краевые условия строится система уравнений, разрешимость которой зависит от невырожденности соответствующей матрицы. Кроме того, рассматривается случай неоднозначности решения, при котором исследуются собственные значения и формулируются условия разрешимости исходной задачи.

1. Przeworska-Rolewicz, D. Equations with Transformed Argument, An Algebraic Approach, 1st ed.; Elsevier Scientific: Amsterdam, The Netherlands, 1973.

2. Wiener, J. Generalized Solutions of Functional Differential Equations, 1st ed., World Scientific: Singapore, River Edge NJ, USA, London, UK Hong Kong, China, 1993.

3. Karapetiants, N., Samko, S. Equations with Involutive Operators, 1st ed. World Birkha¨user: Boston, MA, USA, 2001.

4. Cabada, A., Tojo, F.A.F. Differential Equations with Involutions, 1st ed., Atlantis Press: Paris, France, 2015.

5. Al-Salti, N., Kerbal, S., Kirane, M. Initial-boundary value problems for a time-fractional differential equation with involution perturbation. Math. Model. Nat. Phenomena, 14, 312 (2019).

6. Kritskov, L.V., Sadybekov, M.A., Sarsenbi, A.M. Properties in Lp of root functions for a nonlocal problem with involution. Turk. J. Math., 43, 393–401 (2019).

7. Sarsenbi, A., Sarsenbi, A. On eigenfunctions of the boundary value problems for second order differential equations with involution. Symmetry, 13, 1972 (2021).

8. Turmetov, B., Karachik, V. On eigenfunctions and eigenvalues of a nonlocal Laplace operator with multiple Involution. Symmetry, 13, 1981 (2021).

9. Dildabek, G., Ivanova, M.B., Sadybekov, M.A. On root functions of nonlocal differential secondorder operator with boundary conditions of periodic type. Journal of Mathematics, Mechanics and Computer Science, 112 (4), 29–44 (2021).

10. Dzhumabayev, DS. Criteria for the unique solvability of a linear boundary-value problem for an ordinary differential equation. Comput Maths Math Phys., 29 (34), 34–46 (1989).

11. Assanova, A.T., Bakirova, E.A., Kadirbayeva, Z.M. Numerical Solution to a Control Problem for Integro-Differential Equations, Comput. Math. and Math. Phys., 60 (2), 203–221 (2020).

12. Dzhumabaev, D.S. An algorithm for solving a linear two-point boundary value problem for an integrodifferential equation, Computational Mathematics and Mathematical Physics., 53 (6), 736–758 (2013).